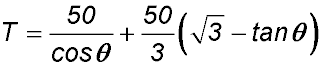Where the techniques of Maths
are explained in simple terms.
Trigonometric functions - differentiation - max/min questions.
Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
| Theoretical | 1. (i) Differentiate y = sin x + cos x.
(ii) Find the minimum point and the point(s) of inflection in the domain 0 ≤ x ≤ 2π. |
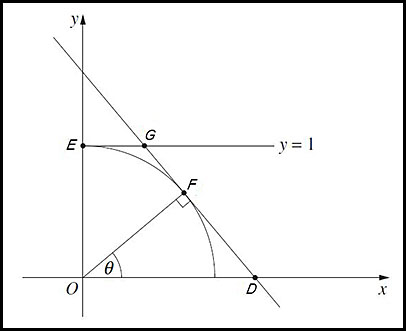
| 2. The diagram shows a point F on the unit circle x2 + y2 = 1 at an angle of θ to the positive direction of the x-axis (0 ≤ θ ≤ π).
The tangent at F is perpendicular to OF. It intersects the x-axis at D and the line y = 1 at G. The line y = 1 intersects the y axis at E.
Answer:Area is min at θ = π/6. |
|
3. Consider the curve y = sin x (1 + cos x) for 0 ≤ x ≤ 2 π.
|
|
| Practical situations | 4. After several days of measurement and testing the waves at Curl Curl Beach before the Trial, Charlie determined that wave height could be modelled by the equation 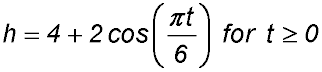
where h is the height of the tide at t hours. Answer:(i) 3 m. (ii) rate was 0.9 m/hour. (iii) at the rate in (ii) is positive, the height is increasing. |
5. 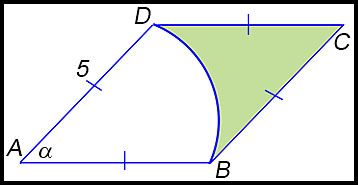
The diagram above shows a rhombus ABCD The sides are each 5 cm long. BD is an arc of a circle centered at A. (i) Show that the area of the coloured region can be expressed as
(ii) Find the maximum area of the coloured region. |
|
| 6. Two sides of a triangle are of lengths 8 cm and 12 cm. The angle between the two sides is θ. Answer:Max area is 48 cm2. |
|
| Type 2: 2D shapes - sectors. |
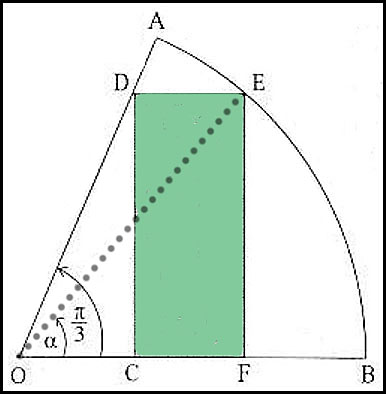
7. AOB is the sector of a circle with centre at O and a radius r. The angle subtended at O by the arc AB is
CDEF is a rectangle drawn in the sector and ∠EOF = α. Answer.(iii) α = π/6. |
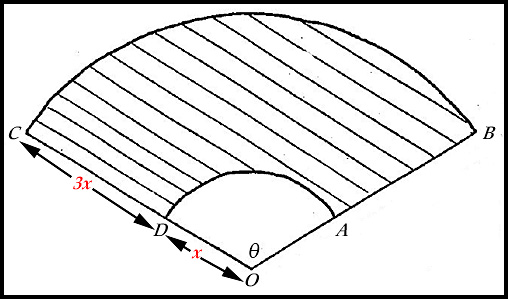
| 8. In the diagram below, a truck's windscreen wiper blade sweeps across the region ABCD where BC and AD are arcs of circles with centre O. The intervals OA and AB are x cm and 3x cm respectively with < BOC = θ.
The perimeter of the shaded region ABCD is 240 cm.
Answer.Max area = 3,600 cm2. |
|
| 9. A sector with an area of 100 cm2 has a radius r and an angle of θ radians.
(i) Show that the perimeter P cm of the sector can be expressed as
(ii) If r and θ vary in such a way that the area of the sector remains constant at 100 cm2, find the radius and the value for θ which give the smallest value for the perimeter. Answer.r = 10 cm and θ = 2 rads. |
|
Type 3: |
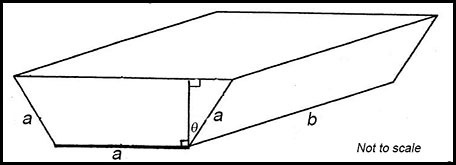
10. A gutter is made out of sheet metal 3a units wide by bending it as shown in the diagram. The length of the gutter is b units.
(i) Show that the volume of the gutter can be expressed as
(ii) Show that (iii) Determine the value of θ so that the gutter has a maximum volume. Answer.Max volume at θ = π/6 rads. |
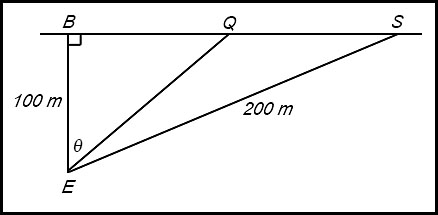
| Type 4: Rates | 11. Evie is at E, shown in the diagram below. At that point, Evie is 100 metres from Point B on the beach.
She decides she wants to use her surfboard which she left at S which is further down the beach and 200 metres from where Evie is now treading water. Evie is a reasonably good athlete. She swims at 2 m/sec and can run at 6 m/sec.
Answer.(iii) Direction is 19o 28'. (iv)Time is 1 min 36 secs. |
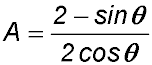
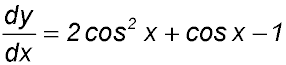
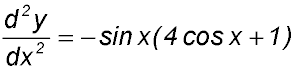 .
.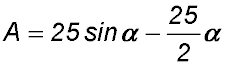
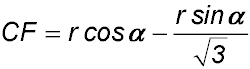 .
.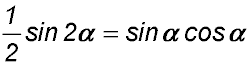 , show that the area of rectangle CDEF can be expressed as .
, show that the area of rectangle CDEF can be expressed as .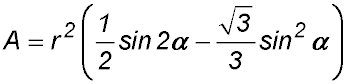
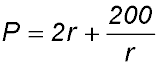
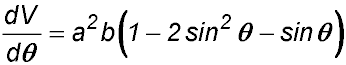 .
.